Risiko und Rendite
Bei der Auswahl eines Portfolios spielen Risiko- und Renditekriterien eine entscheidende Rolle. Da auch Analysten nicht in die Zukunft blicken können, wurden Methoden entwickelt, um auf der Basis von historischen Daten einen durchschnittlichen Erwartungswert µ bzw. E(r) für eine Anlage zu bestimmen. Hierzu werden mögliche Renditen mit Wahrscheinlichkeiten gewichtet, sodass eine zukunftsorientierte erwartete Rendite entsteht:
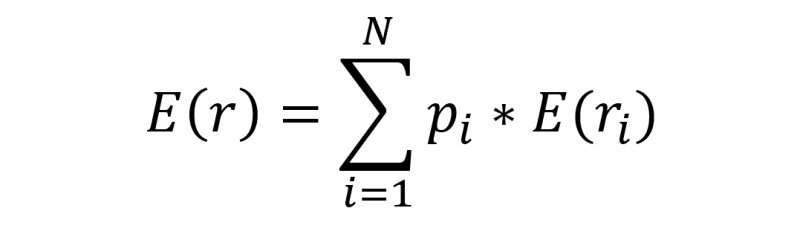
Risiken entstehen aus Volatilitäten der einzelnen Investments: Diese ist ein Maß der Schwankungsintensität eines Kurses und wird in Prozent angegeben. Sie drückt die Möglichkeit von negativen Kursveränderungen aus und wird durch Streuungsmaße quantifiziert. Praktische Anwendung findet hier die normierte Standardabweichung σ als Maß der Volatilität, welche sich aus der Varianz σ² ergibt.
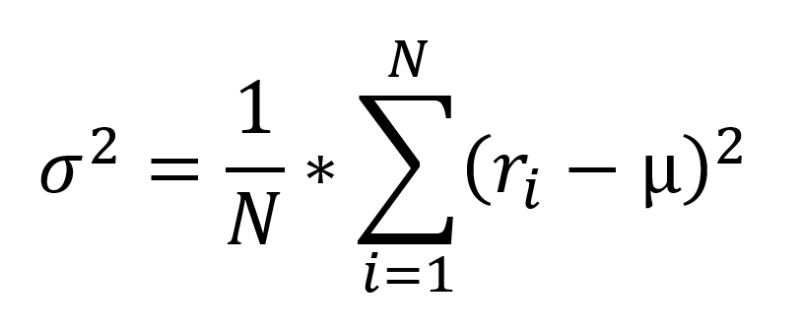

Am Beispiel des DAX wurden für die Jahre von 1997 bis 2016 die jährlichen Renditen ihrer Höhe nach klassiert und in folgendem Histogramm dargestellt:
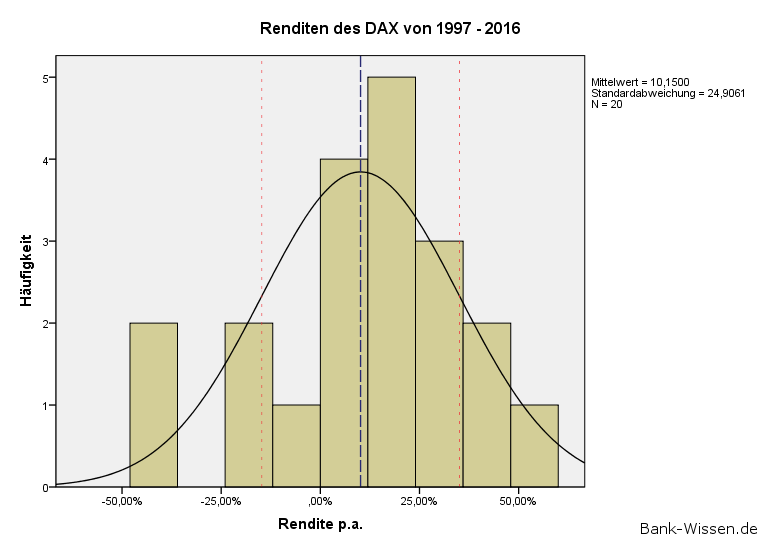
Der Erwartungswert liegt hier bei E(r) = µ = 10,15% p.a. und die Volatilität bei σ = 24,91%.
Hinweis: Der Erwartungswert (ex ante) und die mittlere Rendite (ex post) müssen nicht übereinstimmen, wenn einzelne Faktoren eine andere Erwartung ergeben.
Normalverteilung
Um gezielte Prognosen zu erstellen, können Renditen von Standard-Aktien (z.B. DAX-Aktien) modellhaft als Normalverteilung N(µ,σ) betrachtet werden. Die Kursveränderungen streuen um einen Mittelwert, der sich z.B. durch einen generellen Positivtrend ergibt.
Am Beispiel von historischen 1-Tages-Renditen des DAX lässt sich eine solche Streuung graphisch als Histogramm darstellen. Kleine Renditeveränderungen treten häufiger auf als große Kursgewinne-/verluste, wodurch sich eine typische Verteilung ergibt.
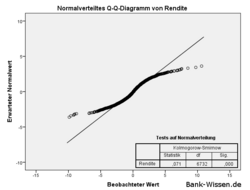
Ein Q-Q-Diagramm und der Kolmogorow-Smirnow-Test zeigen allerdings, dass wir eine Normalverteilung lediglich als starke Vereinfachung von Aktienkursen annehmen dürfen. Dennoch genügt dieses Modell, um einige Annahmen über die Wahrscheinlichkeiten von Kursveränderungen zu treffen.
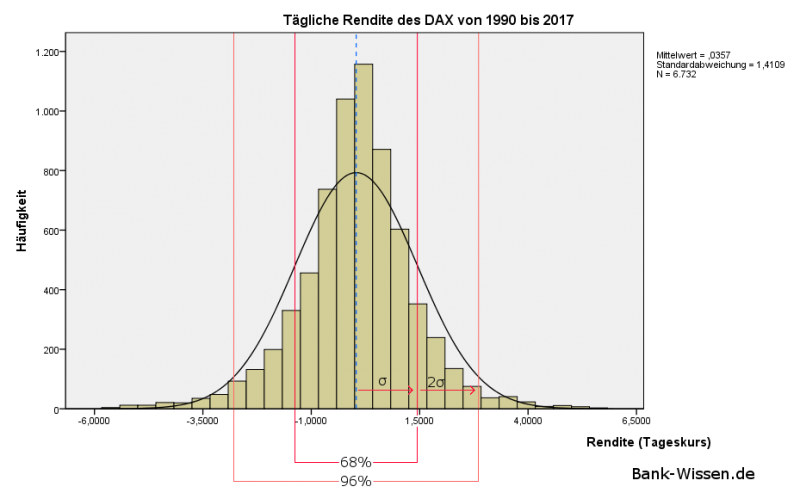
Im Ein-Sigma-Bereich (µ±σ) streuen die tatsächlichen Renditen im Abstand der einfachen Standardabweichung um den Erwartungswert. In diesem Bereich werden bereits 68,27% der Gesamtwahrscheinlichkeit abgebildet.
Analog dazu treten Kursveränderungen im gesamten Zwei-Sigma-Bereich (µ±2*σ) mit 95,45%iger Wahrscheinlichkeit auf. Dass darüber hinaus Kursgewinne oder Kursverluste entstehen kann mit einer Wahrscheinlichkeit von jeweils 2,28% quantifiziert werden (NR: 0,5 - 0,9545/2 = 0,02275). Hierbei handelt es sich um seltenere Ausreißer des Kurses.
Renditeveränderungen, die im Drei-Sigma-Bereich (µ±3*σ) liegen, treten in 99,73% der Fälle auf. Dass Verluste (oder Gewinne) darüber hinaus eintreten, ist daher mit jeweils 0,135% äußerst selten.
Dieses Modell findet in der Praxis häufige Anwendung, da es einfach in der Handhabung ist. Trotz der begrenzten Genauigkeit lässt sich über die Normalverteilungsannahme ein grobes Bild über künftige Renditeerwartungen zeichnen.
Diversifikation
Bestehen Portfolios aus lediglich einem Titel, unterliegen sie der vollkommenen Volatilität dieser einen Aktie. Steigt die Aktie im Kurs um 10%, erhöht sich der Wert des Depots um 10% und umgekehrt. Um das Risiko von Kursverlusten zu kompensieren, sollte ein Portfolio daher aus mehr als einem Titel bestehen.
Eine Methode, um das Portfolio gegen hohe Volatilität bzw. hohe Risiken abzusichern, ist die Auswahl von mehreren Aktien aus unterschiedlichen Branchen, die nicht miteinander korrelieren:
Beispiel:
- Daimler und BMW sind beide Vertreter der Automobilbranche - geht es der Branche generell schlecht, so werden auch beide Aktien fallen. Es besteht somit eine hohe Korrelation (kBMW/Daimler ~ 1).
- Bayer und die Allianz agieren allerdings in völlig verschiedenen Branchen - gibt es erhöhten Druck auf die Pharmaziebranche, hat dies nicht zwangsläufig einen Einfluss auf die Versicherungswirtschaft (kBayer/Allianz ~ 0).
Es wäre theoretisch denkbar, dass zwei Aktien stark negativ korreliert sind (kA/B ~ -1). In diesem Fall können die Risiken bei gleichbleibender Rendite deutlich verringert werden. Dass die zwei Titel allerdings perfekt negativ korreliert sind, ist allerdings eher ein theoretisches Konstrukt. Negative Korrelationen können aber beispielsweise zwischen Rohstoffen und Aktien beobachtet werden. Steigt etwa der Ölpreis, können Aktienkurse fallen, da die Produktion in den Unternehmen verteuert bzw. erschwert wird.
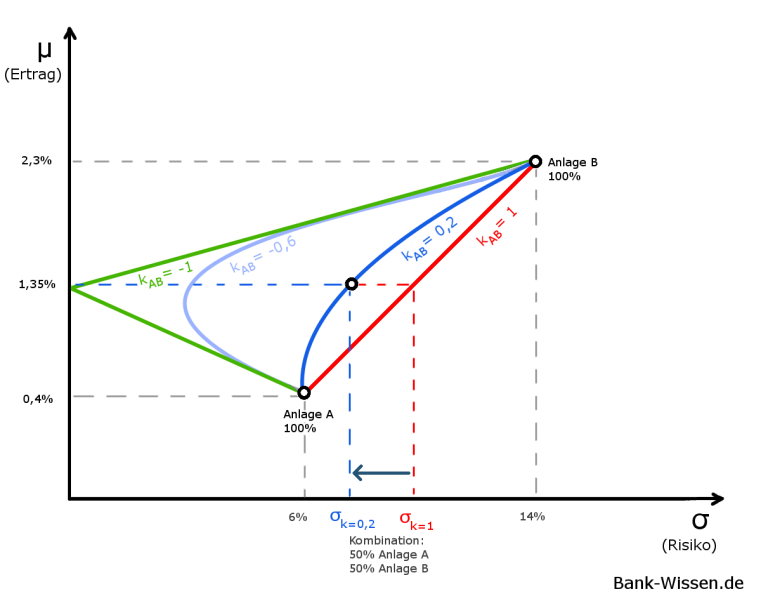
Portfolio-Selection-Modell
Das Portfolio-Selection-Modell strebt nach einem effizienten und optimalen Portfolio. Das Ziel ist es, unter der Auswahl einer persönlichen Risikobereitschaft, das Portfolio mit dem höchsten Ertrag bei gleichbleibendem Risiko zu finden.
Hierfür betrachten wir zunächst mögliche Portfolios in Abhängigkeit vom Risiko:
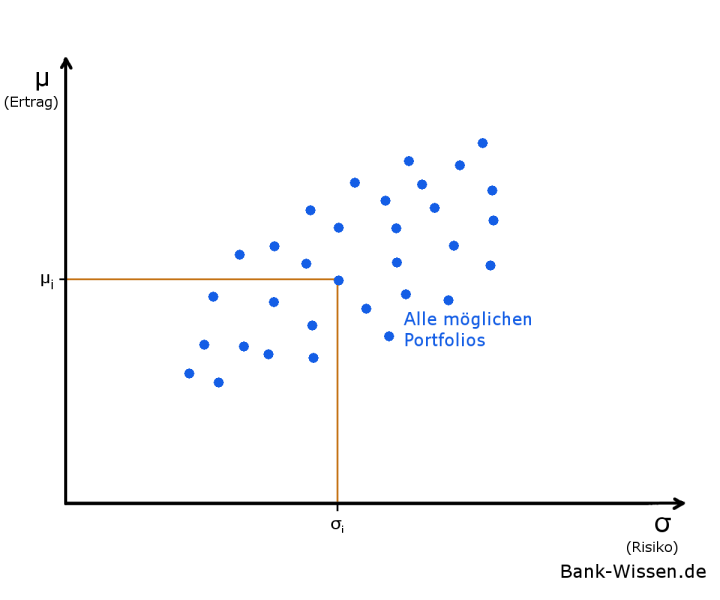
Auf dem Markt existiert eine Vielzahl an Anlagemöglichkeiten, die nicht immer das Ertragspotenzial voll ausnutzen. Der Punkt (σi ; µi) stellt eine ineffiziente Anlagemöglichkeit dar, da es bei gleichem Risiko andere Portfolien mit höheren Erträgen gäbe.
Wir stellen somit fest, dass es verschiedene Anlagemöglichkeiten gibt, die bei gleichem Risiko unterschiedliche Erträge generieren. Nach dem Ökonomen Harry Makrowitz sind allerdings stets die Portfolios auszuwählen, die bei vorgegebenen Risiko die höchsten Erträge erzielen:
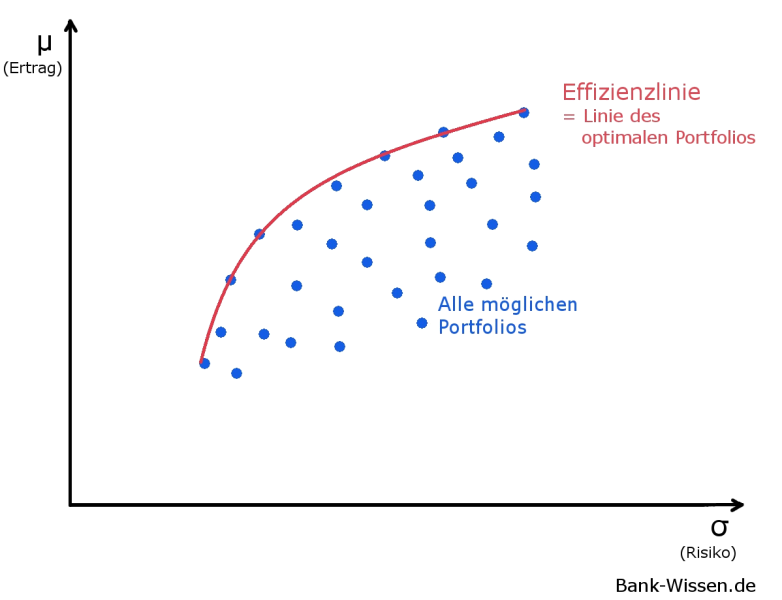
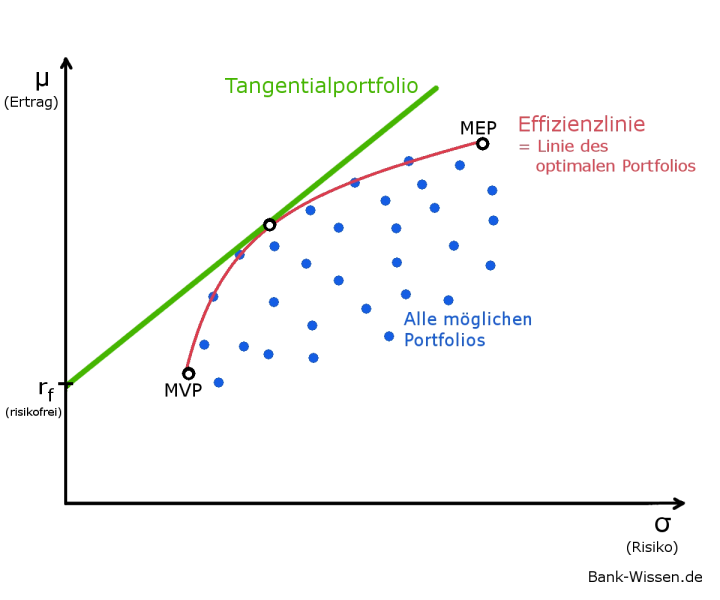
Es ergibt sich oberhalb der Punktwolke (alle möglichen Portfolios) eine Linie, die alle optimalen Portfolios in Abhängigkeit von der Risikobereitschaft darstellt. Diese wird als Effizienzlinie bezeichnet. Portfolios auf dieser Linie sind allen Portfolios unterhalb dieser vorzuziehen.
Das Markt-Portfolio mit dem geringsten Risiko ist das Minimum-Varianz-Portfolio (MVP) und das mit dem größten Ertrag das Maximum-Erfolgs-Portfolio (MEP).
Einige wenige Anlageformen können als nahezu risikofrei angesehen werden. Hiermit sind vorrangig Staatsanleihen von Staaten mit bester Bonität (AAA) mit einer Laufzeit unter 6 Monaten zu verstehen. (Die Einlagenfaszilität der EZB kann ebenfalls als risikofrei angesehen werden.)
Gelingt es dem Anleger nun, mit einer risikolosen Anlage einen Ertrag rf > 0 zu erzielen, so lässt sich ausgehend von diesem Punkt ein Tangentialportfolio konstruieren, das die Effizienzlinie oberhalb schneidet. An diesem Schnittpunkt investiert der Anleger 100% seines Kapitals in ein Portfolio auf der Effizienzlinie. Möchte er sein Risiko verringern, kann er entlang des Tangentialportfolios (nach links) eine Kombination zwischen der risikofreien und der risikobehafteten Anlage auswählen. So ist eine ertragsreichere Anlage oberhalb des MVP zu gleichen Risikobedingungen möglich.
Im Schnittpunkt der Effizienzlinie und des Tangentialportfolios hat der Anleger sein vollständiges Kapital investiert. Darüber hinaus kann es zu weiteren Anlagen kommen, wenn weiteres Kapital mittels Kredit beschafft werden kann. Hier ist vom Leveraging die Rede.